자료구조란?
프로그램에서 사용하기 위한 자료를 기억장치의 공간 내에 저장하는 방법과 저장된 그룹 내에 존재하는 자료 간의 관계, 처리 방법 등을 연구 분석하는 것
선형 구조(Linear Structure)
배열(Array)
선형 리스트(Linear List)
스택(Stack)
큐(Queue)
데크(Deque)
비선형 구조(Non-Linear Structure)
트리(Tree)
그래프(Graph)
자료구조의 활용
정렬(Sort)
검색(Search)
인덱스(Index)
배열(Array)
동일한 자료형의 데이터들이 같은 크기로 나열되어 순서를 갖고 있는 집합
- 정적인 자료구조
- 데이터 삭제 시 삭제된 공간이 빈 공간으로 남아있어 메모리의 낭비가 발생함
- 반복적인 데이터 처리 작업에 적합
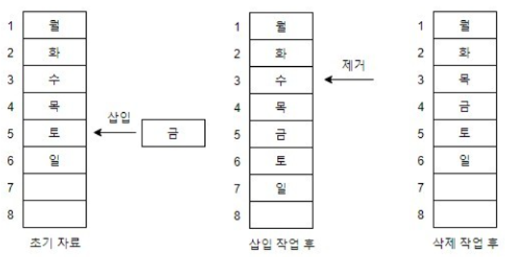
선형 리스트(Linear List)
일정한 순서에 의해 나열된 자료구조
- 연속 리스트(Contiguous List)
- 배열과 같이 연속되는 기억장소에 저장되는 자료구조
- 빈 공간이 있어야 삽입/삭제 시 자료의 이동이 필요

- 연결 리스트(Linked List)
- 자료들을 반드시 연속적으로 배열시키지 않고, 자료 항목의 순서에 따라 노드의 포인터 부분을 이용하여 서로 연결시킨 자료 구조
- 노드의 삽입/삭제 작업이 용이

스택(Stack)
리스트의 한쪽 끝으로만 자료의 삽입, 삭제 작업이 이루어지는 자료 구조
- 가장 나중에 삽입된 자료가 가장 먼저 삭제되는 후입선출(LIFO : Last In First Out) 방식으로 자료 처리
- 스택의 모든 공간이 꽉 채워져 있는 상태에서 데이터 삽입 → 오버플로(Overflow) 발생
- 더 이상 삭제할 데이터가 없는 상태에서 데이터를 삭제 → 언더플로(Underflow) 발생

- TOP : 가장 마지막으로 삽입된 자료가 기억된 위치를 가리키는 요소
- Bottom : 스택의 가장 밑바닥
큐(Queue)
리스트의 한쪽에서는 삽입 작업이 이루어지고 다른 한쪽에서는 삭제 작업이 이루어지도록 구성한 자료 구조
- 가장 먼저 삽입된 자료가 가장 먼저 삭제되는 선입선출(FIFO : First In First Out)방식으로 처리
- 시작과 끝을 표시하는 두 개의 포인터가 있음
- 프런트(F, Front) 포인터
- 가장 먼저 삽입된 자료의 기억 공간을 가리키는 포인터
- 리어(R, Rear) 포인터
- 가장 마지막에 삽입된 자료가 위치한 기억 공간을 가리키는 포인터로 삽입 작업을 할 때 사용
- 프런트(F, Front) 포인터
- 운영체제의 작업 스케줄링에 사용

데크(Deque)
삽입과 삭제가 리스트의 양쪽 끝에서 모두 발생할 수 있는 자료구조
- Stack과 Queue의 장점만 따서 구성한 것

트리(Tree)
정점(Node)과 선분(Branch)을 이용하여 사이클을 이루지 않도록 구성한 그래프의 특수한 형태
- 하나의 기억 공간 → 노드(Node)
- 노드와 노드를 연결하는 선 → 링크(Link)

- 노드(Node) : 트리의 기본 요소, 가지를 합친 것
- ex) A, B, C, D, E, F, G, H, I, J, K, L, M
- 근 노드(Root Node) : 트리의 맨 위에 있는 노드
- ex) A
- 디그리(Degree, 차수) : 각 노드에서 뻗어 나온 가지의 수
- ex) A = 3, B = 2, C = 1, D = 3
- 단말 노드(Terminal Node) = 잎 노드(Leaf Node) : 자식이 하나도 없는 노드, 즉 디그리 0인 노드
- ex) K, L, F, G, M, I, J
- 자식 노드(Son Node) : 어떤 노드에 연결된 다음 레벨의 노드들
- ex) D의 자식 노드 : H, I, J
- 부모 노드(Parent Node) : 어떤 노드에 연결된 이전 레벨의 노드들
- ex) E, F의 부모 노드 : B
- 형제 노드(Brother Node, Sibling) : 동일한 부모를 갖는 노드들
- ex) H의 형제 노드 : I, J
- 트리의 디그리 : 노드들의 디그리 중에서 가장 많은 수
- ex) 노드 A나 D가 3개의 디그리를 가지므로 앞 트리의 디그리는 3
그래프(Graph)
그래프 G는 정점 V와 간선 E의 두 집합
- 간선의 방향성 유무에 따라 방향 그래프와 무방향 그래프로 구분
- 트리(Tree)는 사이클이 없는 그래프(Graph)

- n개의 정점으로 구성된 무방향 그래프의 최대 간선 수 → n(n-1)/2
- n개의 정점으로 구성된 방향 그래프의 최대 간선 수 → n(n-1)
정점이 4개인 경우
→ 무방향 그래프의 최대 간선 수 : 4(4-1)/2 = 6
→ 방향 그래프의 최대 간선 후 : 4(4-1) = 12
'CS 지식 > [자료구조]' 카테고리의 다른 글
| [자료구조] 제네릭(generic) (0) | 2023.10.20 |
|---|---|
| [자료구조] 빅오 표기법(big-O notation) (1) | 2023.10.20 |
| [자료구조] HashMap (0) | 2023.08.01 |
| [자료구조] 해시(Hash) (0) | 2023.07.19 |
| [자료구조] 이진 탐색 트리(Binary Search Tree) (0) | 2023.07.19 |